Uma das dúvidas mais comuns em inferência estatística é decidir entre o Teste Z e o Teste t de Student ao realizar um teste de hipóteses para a média de uma população. Embora ambos os testes sejam semelhantes, a escolha correta depende de uma condição fundamental: o conhecimento sobre o desvio padrão da população.
Este guia prático irá detalhar as diferenças, mostrar quando usar cada um e guiar você através de um exemplo completo, resolvido à mão e com código em Julia.
Uma Breve História: De Gauss a Gosset
Para entender a diferença entre os testes, é útil conhecer suas origens.
O Teste Z é o mais antigo dos dois, fundamentado na distribuição normal, também conhecida como curva de Gauss. A teoria por trás dela foi desenvolvida por matemáticos como Abraham de Moivre, Pierre-Simon Laplace e Carl Friedrich Gauss nos séculos XVIII e XIX. O Teste Z tornou-se uma ferramenta padrão para a estatística porque, sob certas condições (como o Teorema Central do Limite), muitas médias amostrais se comportam de acordo com essa distribuição. Sua principal premissa, no entanto, sempre foi uma grande limitação: ele exige que conheçamos o verdadeiro desvio padrão da população ($\sigma$), um parâmetro que raramente está disponível no mundo real.
A solução para esse problema surgiu no início do século XX, em um lugar inesperado: a Cervejaria Guinness, em Dublin. William Sealy Gosset, um químico e estatístico que trabalhava para a Guinness, enfrentava um desafio prático: como testar a qualidade de lotes de cevada usando apenas amostras pequenas? O Teste Z não era adequado, pois o desvio padrão da população era desconhecido.
Gosset dedicou-se a resolver essa questão e, em 1908, publicou sua descoberta sob o pseudônimo de “Student” (a Guinness não permitia que seus funcionários publicassem pesquisas em seus próprios nomes para proteger segredos comerciais). Ele desenvolveu uma nova distribuição, a distribuição t de Student, que se ajusta à incerteza de estimar o desvio padrão a partir de uma amostra pequena. Assim nasceu o Teste t, uma das ferramentas mais importantes e amplamente utilizadas na estatística moderna, permitindo que pesquisadores tirem conclusões robustas mesmo com dados limitados.
A Diferença Fundamental: $\sigma$ Conhecido vs. Desconhecido
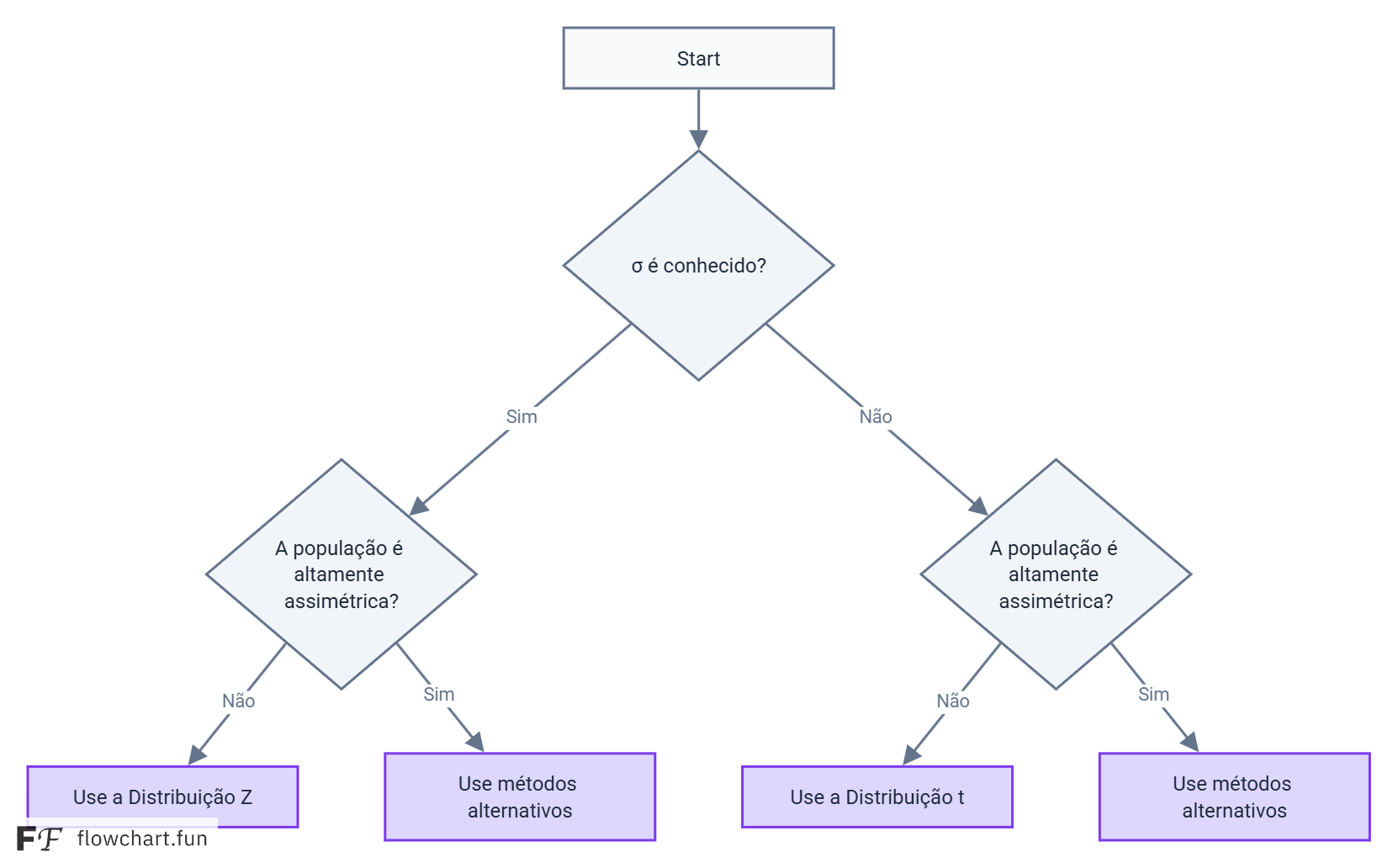
A regra de ouro para escolher entre os testes é simples:
- Use o Teste Z quando:
- O desvio padrão da população ($\sigma$) é conhecido.
- OU o tamanho da amostra ($n$) é grande (geralmente $n > 30$), e o desvio padrão da população é desconhecido. Pelo Teorema Central do Limite, a distribuição das médias amostrais se aproxima da normal, e o desvio padrão da amostra ($s$) se torna uma estimativa confiável de $\sigma$.
- Use o Teste t de Student quando:
- O desvio padrão da população ($\sigma$) é desconhecido.
- O tamanho da amostra ($n$) é pequeno (geralmente $n \le 30$).
A distribuição t de Student é mais “achatada” e com caudas mais pesadas que a distribuição normal padrão (Z), o que reflete a incerteza adicional de ter que estimar o desvio padrão da população a partir da amostra.
Exemplo Prático: Altura Média de Estudantes
Uma pesquisadora de uma universidade quer verificar se a altura média dos estudantes do primeiro ano é diferente da média nacional, que é de 175 cm. Ela coleta uma amostra aleatória de 25 estudantes e obtém os seguintes resultados:
- Média da amostra ($\bar{x}$): 178 cm
- Desvio padrão da amostra ($s$): 8 cm
Ela decide usar um nível de significância de $\alpha = 0.05$.
Cenário 1: Teste Z (Desvio Padrão da População Conhecido)
Vamos supor um cenário hipotético onde um estudo nacional anterior determinou que o desvio padrão da altura de todos os estudantes universitários do país é $\sigma = 7$ cm.
1. Definir as Hipóteses
- Hipótese Nula ($H_0$): A altura média dos estudantes é igual à média nacional. \(H_0: \mu = 175 \text{ cm}\)
- Hipótese Alternativa ($H_1$): A altura média é diferente da média nacional (teste bilateral). \(H_1: \mu \neq 175 \text{ cm}\)
2. Calcular a Estatística de Teste Z
\[Z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}} = \frac{178 - 175}{7 / \sqrt{25}} = \frac{3}{7 / 5} = \frac{3}{1.4} \approx 2.14\]3. Determinar o Valor Crítico e o P-valor
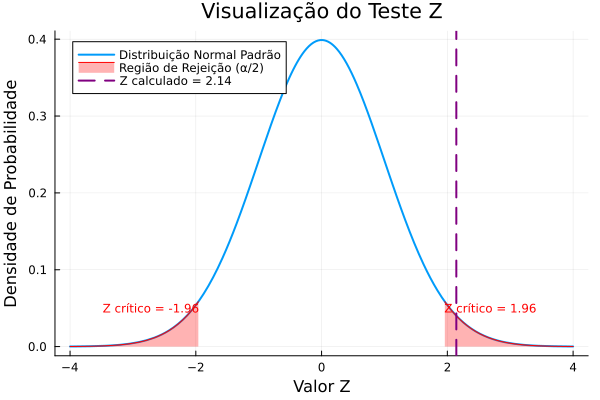
- Valor Crítico: Para um teste bilateral com $\alpha = 0.05$, olhamos a área de $\alpha/2 = 0.025$ em cada cauda. O valor Z crítico correspondente é $\pm 1.96$.
- P-valor: É a probabilidade de observar um valor Z tão extremo ou mais extremo que 2.14. $P(Z > 2.14) \approx 0.0162$. Como o teste é bilateral, multiplicamos por 2: p-valor = $2 \times 0.0162 = 0.0324$.
4. Tomar a Decisão
- Comparando a estatística de teste: Nosso Z calculado (2.14) é maior que o Z crítico (1.96). Ele cai na região de rejeição.
- Comparando o p-valor: Nosso p-valor (0.0324) é menor que o nível de significância $\alpha$ (0.05).
Ambas as abordagens levam à mesma conclusão: rejeitamos a hipótese nula ($H_0$).
5. Intervalo de Confiança (95%)
O intervalo de confiança nos dá uma faixa de valores onde acreditamos que a verdadeira média da população se encontra.
a) Intervalo Bilateral (Two-Sided)
Fórmula:
\[IC = \bar{x} \pm Z_{\alpha/2} \cdot \left(\frac{\sigma}{\sqrt{n}}\right)\]Cálculo: Substituindo os valores ($\bar{x}=178$, $\sigma=7$, $n=25$) e o valor Z-crítico para um teste bilateral ($Z_{0.025} = 1.96$):
\[\begin{align*} IC &= 178 \pm 1.96 \cdot \left(\frac{7}{\sqrt{25}}\right) \\ &= 178 \pm 1.96 \cdot \left(\frac{7}{5}\right) \\ &= 178 \pm 1.96 \cdot (1.4) \\ &= 178 \pm 2.744 \end{align*}\]Isso nos dá os seguintes limites:
- Limite Inferior: $178 - 2.744 = 175.256$
- Limite Superior: $178 + 2.744 = 180.744$
Resultado: Arredondando, o intervalo de confiança de 95% é [175.26, 180.74].
b) Intervalos Unilaterais (One-Sided)
Para hipóteses direcionais, usamos o Z-crítico que coloca toda a área de $\alpha$ (0.05) em uma única cauda: $Z_{\alpha} = Z_{0.05} = 1.645$.
-
Unilateral à Direita (Limite Inferior): \(\text{Limite Inferior} = \bar{x} - Z_{\alpha} \cdot \left(\frac{\sigma}{\sqrt{n}}\right) = 178 - 1.645 \cdot 1.4 = 178 - 2.303 = 175.697\) Resultado: Temos 95% de confiança de que a altura média é de pelo menos 175.70 cm, ou [175.70, +∞).
-
Unilateral à Esquerda (Limite Superior): \(\text{Limite Superior} = \bar{x} + Z_{\alpha} \cdot \left(\frac{\sigma}{\sqrt{n}}\right) = 178 + 1.645 \cdot 1.4 = 178 + 2.303 = 180.303\) Resultado: Temos 95% de confiança de que a altura média é de no máximo 180.30 cm, ou (-∞, 180.30].
Como o valor da hipótese nula (175) não está dentro do intervalo de confiança bilateral, isso reforça nossa decisão de rejeitar $H_0$.
6. Resolução em Julia (Teste Z)
using HypothesisTests, Distributions
# Parâmetros do problema
μ₀ = 175 # Média sob H₀
x̄ = 178 # Média da amostra
σ = 7 # Desvio padrão populacional CONHECIDO
n = 25 # Tamanho da amostra
# Realizando o Teste Z para uma amostra
ztest = OneSampleZTest(x̄, σ, n, μ₀)
p_valor = pvalue(ztest)
z_stat = ztest.z
ci = confint(ztest)
println("--- Resultados do Teste Z ---")
println("Estatística Z calculada: ", round(z_stat, digits=3))
println("P-valor: ", round(p_valor, digits=3))
println("Intervalo de Confiança (95%): [", round(ci[1], digits=2), ", ", round(ci[2], digits=2), "]")
Gráfico Gerado:
Cenário 2: Teste t de Student (Desvio Padrão da População Desconhecido)
Agora, vamos ao cenário mais realista: a pesquisadora não conhece o desvio padrão da população ($\sigma$) e deve usar o desvio padrão da sua amostra, $s = 8$ cm.
1. Definir as Hipóteses
As hipóteses são as mesmas: \(H_0: \mu = 175 \text{ cm}\) \(H_1: \mu \neq 175 \text{ cm}\)
2. Calcular a Estatística de Teste t
Os graus de liberdade são $gl = n - 1 = 25 - 1 = 24$.
\[t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} = \frac{178 - 175}{8 / \sqrt{25}} = \frac{3}{8 / 5} = \frac{3}{1.6} = 1.875\]3. Determinar o Valor Crítico e o P-valor
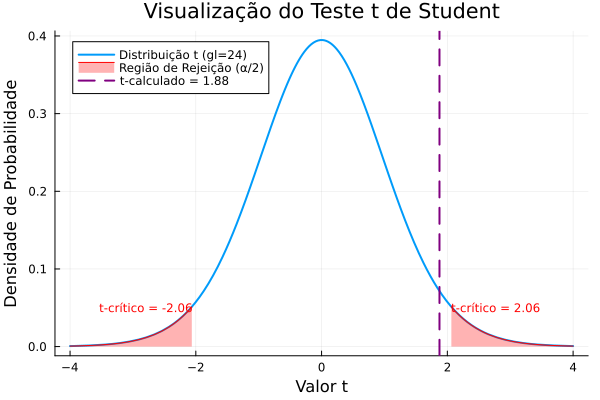
- Valor Crítico: Para um teste bilateral com $\alpha = 0.05$ e 24 graus de liberdade, consultamos a tabela t de Student. O valor t crítico é $\pm 2.064$.
- P-valor: É a probabilidade de observar um valor t tão extremo ou mais extremo que 1.875. Usando software, encontramos p-valor $\approx 0.072$.
4. Tomar a Decisão
- Comparando a estatística de teste: Nosso t calculado (1.875) é menor que o t crítico (2.064). Ele não cai na região de rejeição.
- Comparando o p-valor: Nosso p-valor (0.072) é maior que o nível de significância $\alpha$ (0.05).
Ambas as abordagens levam à mesma conclusão: falhamos em rejeitar a hipótese nula ($H_0$).
5. Intervalo de Confiança (95%)
O intervalo de confiança nos dá uma faixa de valores onde acreditamos que a verdadeira média da população se encontra, com um certo nível de confiança.
a) Intervalo Bilateral (Two-Sided)
Este é o tipo mais comum, usado para estimar que a média está entre dois valores.
Fórmula:
\[IC = \bar{x} \pm t_{\alpha/2, gl} \cdot \left(\frac{s}{\sqrt{n}}\right)\]Cálculo: Substituindo os valores da nossa amostra ($\bar{x}=178$, $s=8$, $n=25$) e o valor t-crítico para um teste bilateral ($t_{0.025, 24} = 2.064$):
\[\begin{align*} IC &= 178 \pm 2.064 \cdot \left(\frac{8}{\sqrt{25}}\right) \\ &= 178 \pm 2.064 \cdot \left(\frac{8}{5}\right) \\ &= 178 \pm 2.064 \cdot (1.6) \\ &= 178 \pm 3.3024 \end{align*}\]Isso nos dá os seguintes limites:
- Limite Inferior: $178 - 3.3024 = 174.6976$
- Limite Superior: $178 + 3.3024 = 181.3024$
Resultado: Arredondando para duas casas decimais, o intervalo de confiança de 95% é [174.70, 181.30].
b) Intervalos Unilaterais (One-Sided)
Usamos um intervalo unilateral quando nossa hipótese é direcional (apenas maior que ou apenas menor que). Para isso, usamos um t-crítico diferente, que coloca toda a área de $\alpha$ (0.05) em uma única cauda: $t_{\alpha, gl} = t_{0.05, 24} = 1.711$.
-
Unilateral à Direita (Limite Inferior): Se quiséssemos ter 95% de confiança de que a média é pelo menos um certo valor.
\[\text{Limite Inferior} = \bar{x} - t_{\alpha, gl} \cdot \left(\frac{s}{\sqrt{n}}\right) = 178 - 1.711 \cdot 1.6 = 178 - 2.7376 = 175.26\]Resultado: Temos 95% de confiança de que a altura média é de pelo menos 175.26 cm, ou [175.26, +∞).
-
Unilateral à Esquerda (Limite Superior): Se quiséssemos ter 95% de confiança de que a média é no máximo um certo valor.
\(\text{Limite Superior} = \bar{x} + t_{\alpha, gl} \cdot \left(\frac{s}{\sqrt{n}}\right) = 178 + 1.711 \cdot 1.6 = 178 + 2.7376 = 180.74\) Resultado: Temos 95% de confiança de que a altura média é de no máximo 180.74 cm, ou (-∞, 180.74].
O valor da hipótese nula (175) está dentro do intervalo de confiança, o que confirma nossa decisão de não rejeitar $H_0$.
Conclusão do Exemplo: Note como a incerteza adicional (usar $s$ em vez de $\sigma$) levou a uma conclusão diferente. O Teste t é mais conservador, exigindo uma evidência mais forte para rejeitar a hipótese nula.
Resolução em Julia (Teste t)
Vamos resolver o cenário realista (Teste t) usando Julia, incluindo um gráfico para visualização.
using HypothesisTests, Distributions, Plots
# Parâmetros do problema
μ₀ = 175 # Média sob H₀
x̄ = 178 # Média da amostra
s = 8 # Desvio padrão da amostra
n = 25 # Tamanho da amostra
α = 0.05 # Nível de significância
# Realizando o Teste t de Student para uma amostra
# Nota: A função OneSampleTTest espera os dados, mas podemos passar as estatísticas
# criando um objeto T-Test manualmente para obter os resultados.
ttest = OneSampleTTest(x̄, s, n, μ₀)
p_valor = pvalue(ttest)
t_stat = ttest.t
gl = n - 1
ci = confint(ttest)
println("--- Resultados do Teste t de Student ---")
println("Estatística t calculada: ", round(t_stat, digits=3))
println("Graus de Liberdade: ", gl)
println("P-valor: ", round(p_valor, digits=3))
println("Intervalo de Confiança (95%): [", round(ci[1], digits=2), ", ", round(ci[2], digits=2), "]")
# Visualização Gráfica
dist = TDist(gl)
t_critico = quantile(dist, 1 - α/2)
plot(x -> pdf(dist, x), -4, 4, label="Distribuição t (gl=$gl)",
xlabel="Valor t", ylabel="Densidade de Probabilidade",
title="Visualização do Teste t de Student",
linewidth=2, legend=:topleft)
# Área de rejeição (cauda direita)
plot!(x -> pdf(dist, x), t_critico, 4, fill=(0, 0.3, :red),
label="Região de Rejeição (α/2)", color=:red)
# Área de rejeição (cauda esquerda)
plot!(x -> pdf(dist, x), -4, -t_critico, fill=(0, 0.3, :red),
label="", color=:red)
# Linha da estatística de teste
vline!([t_stat], color=:purple, linestyle=:dash, linewidth=2,
label="t-calculado = $(round(t_stat, digits=2))")
annotate!(-t_critico, 0.05, text("t-crítico = -$(round(t_critico, digits=2))", :red, :right, 8))
annotate!(t_critico, 0.05, text("t-crítico = $(round(t_critico, digits=2))", :red, :left, 8))
Saída esperada:
Gráfico Gerado:
Apêndice: O Que Fazer com Valores Z Extremos?
Às vezes, ao calcular a estatística de teste, você pode obter um valor Z que está muito fora do intervalo das tabelas padrão (que geralmente vão de -3.99 a +3.99). O que isso significa?
Vamos usar o exemplo de um Z-calculado = -6.36.
👉 Por que não está na tabela?
A tabela Z mostra a probabilidade acumulada até um certo valor. Um valor de Z = -6.36 significa que a observação está 6.36 desvios padrão abaixo da média — uma região de probabilidade extremamente baixa e rara.
Cálculo da Probabilidade (P-valor)
Para um valor tão extremo, o p-valor (a área na cauda) será praticamente zero. Usando software ou uma aproximação analítica, encontramos:
\[P(Z < -6.36) \approx 1.0 \times 10^{-10}\]Isso é 0.0000000001.
💡 Interpretação Prática: Em um teste de hipóteses, um p-valor tão pequeno é uma evidência extremamente forte contra a hipótese nula. Para todos os fins práticos, podemos considerar o p-valor como sendo zero.
Cálculo Manual (Aproximação da Cauda)
É possível estimar essa probabilidade manualmente. O objetivo é calcular a área acumulada até -6.36, que é representada pela integral da função de densidade da normal padrão:
\[P(Z < -6.36) = \int_{-\infty}^{-6.36} \frac{1}{\sqrt{2\pi}} e^{-z^2/2} dz\]Não é possível resolver essa integral exatamente à mão, mas há aproximações precisas para valores extremos.
Passo 1 – Fórmula de Aproximação
Para um valor $z$ muito negativo ($z < -3$), a probabilidade acumulada $P(Z < z)$ pode ser aproximada por:
\[P(Z < z) \approx \frac{1}{\sqrt{2\pi}} \frac{e^{-z^2/2}}{|z|}\]Passo 2 – Substituindo $z = -6.36$
-
Calcule $z^2$: $(-6.36)^2 = 40.4496$
-
Calcule $e^{-z^2/2}$: $e^{-40.4496 / 2} = e^{-20.2248} \approx 1.64 \times 10^{-9}$
-
Substitua na fórmula:
\[P(Z < -6.36) \approx \frac{1}{\sqrt{2\pi}} \cdot \frac{1.64 \times 10^{-9}}{|-6.36|}\]Sabendo que $\frac{1}{\sqrt{2\pi}} \approx 0.39894$:
\[P(Z < -6.36) \approx 0.39894 \cdot \frac{1.64 \times 10^{-9}}{6.36}\] \[P(Z < -6.36) \approx 0.39894 \cdot (2.58 \times 10^{-10}) \approx 1.03 \times 10^{-10}\]
Resultado final:
\[P(Z < -6.36) \approx 0.0000000001\]ou seja,
\[\Phi(-6.36) \approx 1.0 \times 10^{-10}\]Isso confirma que a chance de observar um resultado tão extremo é menor que uma em 10 bilhões, reforçando a decisão de rejeitar a hipótese nula com altíssima confiança.
Resumo Final
| Característica | Teste Z | Teste t de Student |
|---|---|---|
| Condição Principal | $\sigma$ (desvio padrão populacional) é conhecido | $\sigma$ é desconhecido |
| Uso Secundário | Amostra grande ($n > 30$) | Amostra pequena ($n \le 30$) |
| Distribuição de Referência | Normal Padrão (Z) | t de Student (com $n-1$ graus de liberdade) |
| Fórmula da Estatística | $$Z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}}$$ | $$t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}$$ |
| Conservadorismo | Menos conservador | Mais conservador (exige evidência mais forte) |
🎧 Podcast: Aprofundando em Teste Z vs Teste t de Student
Para uma discussão mais aprofundada sobre o tema, ouça o nosso podcast. Cobrimos exemplos práticos e dicas para escolher a distribuição correta para seus dados.
Referências
- Student. (1908). The probable error of a mean. Biometrika, 6(1), 1–25.
- Wikipedia contributors. (2025). Z-test. Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/wiki/Z-test
- Wikipedia contributors. (2025). Student’s t-test. Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/wiki/Student%27s_t-test
- Montgomery, D. C., & Runger, G. C. (2018). Applied Statistics and Probability for Engineers. John Wiley & Sons.
